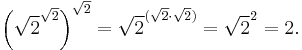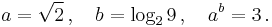Constructive proof

In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object. This is in contrast to a non-constructive proof (also known as an existence proof or pure existence theorem) which proves the validity of a proposition without considering an example.

Some non-constructive proofs show that if a certain proposition is false, a contradiction ensues; consequently the proposition must be true (proof by contradiction). Nearly every proof which explicitly relies on the axiom of choice is non-constructive in nature because this axiom is fundamentally non-constructive. The same can be said for proofs invoking König's lemma.

Constructivism is the philosophy that rejects all but constructive proofs in mathematics. Typically, supporters of this view deny that pure existence can be usefully characterized as "existence" at all: accordingly, a non-constructive proof is instead seen as "refuting the impossibility" of a mathematical object's existence, a strictly weaker statement.

Constructive proofs can be seen as defining certified mathematical algorithms: this idea is explored in the Brouwer–Heyting–Kolmogorov interpretation of constructive logic, the Curry–Howard correspondence‎ between proofs and programs, and such logical systems as Per Martin-Löf's Intuitionistic Type Theory, and Thierry Coquand and Gérard Huet's Calculus of Constructions.

1 Example
2 Brouwerian counterexamples
3 References
4 Further reading

Example

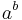Consider the theorem "There exist irrational numbers $a$ and $b$ such that $a^b$ is rational." This theorem can be proved via a constructive proof, or via a non-constructive proof.

Jarden's non-constructive proof proceeds as follows:^[1]

Recall that 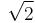$\sqrt{2}$ is irrational, and 2 is rational. Consider the number 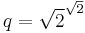$q = \sqrt{2}^{\sqrt2}$ . Either it is rational or it is irrational.

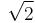If $q$ is rational, then the theorem is true, with $a$ and $b$ both being $\sqrt{2}$ .

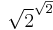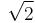If $q$ is irrational, then the theorem is true, with $a$ being $\sqrt{2}^{\sqrt2}$ and $b$ being $\sqrt{2}$ , since

$\left (\sqrt{2}^{\sqrt2}\right )^{\sqrt2} = \sqrt{2}^{(\sqrt{2} \cdot \sqrt{2})} = \sqrt{2}^2 = 2.$

This proof is non-constructive because it relies on the statement "Either q is rational or it is irrational"—an instance of the law of excluded middle, which is not valid within a constructive proof. The non-constructive proof does not construct an example a and b; it merely gives a number of possibilities (in this case, two mutually exclusive possibilities) and shows that one of them—but does not show which one—must yield the desired example.

(It turns out that 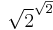$\sqrt{2}^{\sqrt2}$ is irrational because of the Gelfond–Schneider theorem, but this fact is irrelevant to the correctness of the non-constructive proof.)

A constructive proof of the theorem would give an actual example, such as:

$a = \sqrt{2}\, , \quad b = \log_2 9\, , \quad a^b = 3\, .$

The square root of 2 is irrational, and 3 is rational. 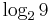$\log_2 9$ is also irrational: if it were equal to 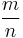$m \over n$ , then, by the properties of logarithms, 9ⁿ would be equal to 2^m, but the former is odd, and the latter is even.

A more substantial example is the graph minor theorem. A consequence of this theorem is that a graph can be drawn on the torus if, and only if, none of its minors belong to a certain finite set of "forbidden minors". However, the proof of the existence of this finite set is not constructive, and the forbidden minors are not actually specified. They are still unknown.

Brouwerian counterexamples

In constructive mathematics, a statement may be disproved by giving a counterexample, as in classical mathematics. However, it is also possible to give a Brouwerian counterexample to show that the statement is essentially non-constructive. This sort of counterexample shows that the statement implies some principle that is known to be non-constructive. For example, a particular statement may be shown to imply the law of the excluded middle. If it can be proved constructively that a statement implies some principle that is not constructively provable, then the statement itself cannot be constructively provable. An example of a Brouwerian counterexample is Diaconescu's theorem showing that the full axiom of choice is non-constructive since it implies the law of excluded middle. A weak Brouwerian counterexample does not disprove a statement, however; it only shows that the statement has no constructive proof.

On the other hand Brouwer gives strong counterexamples, based on properties that hold only in his constructive mathematics. He uses strong counterexamples to show that the law of the excluded middle cannot hold. One of these properties is that two rational numbers can only be proved to be the same if every digit in the decimal expansion can be proved to be the same. If we define a decimal expansion such that some digit is dependent on some yet unsolved mathematical problem, we know beforehand that we cannot tell if this number is the same as some other decimal expansion which is independent of this problem. If the law of the excluded middle would hold - if we could say whether or not the two numbers are the same, that would mean we could solve the yet unsolved problem, which is not the case, so we have disproved the law of the excluded middle.

References

^ George, Alexander; Velleman, Daniel J. (2002). Philosophies of mathematics. Blackwell. pp. 3–4. ISBN 0-631-19544-0.

Constructive proof

Contents

Example

Brouwerian counterexamples

References

Further reading